Druk: Toepassing
1. Herhaling Formules
1.1. druk, algemeen
- \(p=\frac{F}{A} \quad \) met eenheid Pascal: \(\left[Pa = \frac{N}{m^2} = \frac{kg}{m\cdot s^2}\right]\)
- LB Th1 H1 ↗13
1.2. hydrostatische druk:
- \(p = \rho \cdot g \cdot h\)
- LB Th1 H3.1 ↗21
1.3. oefening: hoe hoog is de atmosfeer?
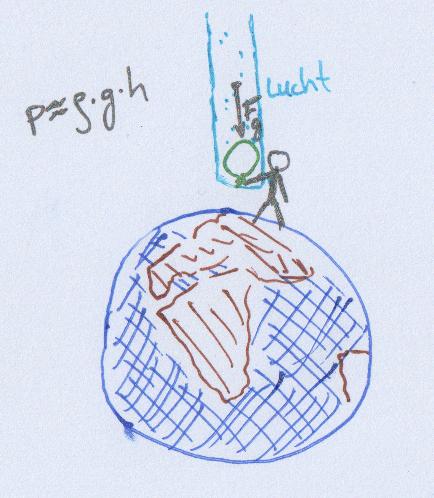
We meten op de aardoppervlakte een druk van \(p = 101,325\ kPa\). De massadichtheid van lucht bedraagt ongeveer \(\rho_{lucht} = 1,2\ \frac{kg}{m^3}\); de valversnelling \(g = 10\ \frac{m}{s^2}\).
- Schat hiermee de hoogte van de atmosfeer!
- Doordenker: waar zitten er foute aannames in deze schatting?
2. Beginsel van Pascal (LB Th1 H3.2 ↗24)
- houder/fles, afgesloten, met gas of vloeistof
- kracht erop: druk!
- (streng genomen: geen gravitatie, geen interacties tussen molecules)
→ druk is overal in de fles hetzelfde
Beginsel/Principe van Pascal:
Een druk uitgeoefend op een deel van een vloeistof in een afgesloten ruimte plant zich met dezelfde grootte in alle richtingen voort in heel de vloeistof.
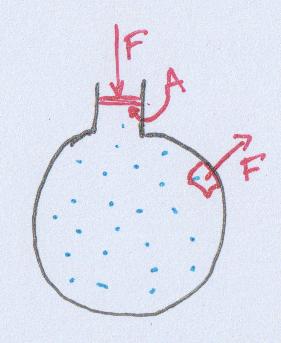
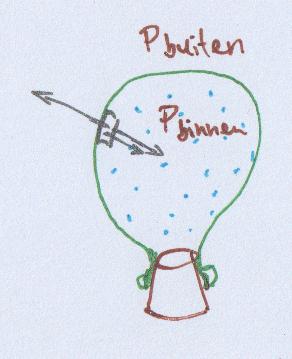
Druk is een scalair = een meetwaarde “zonder (specifieke) richting”.
3. Toepassing: Luchtballon
3.1. een beetje lucht
- Welke krachten zijn aanwezig?
- Wat weten we over de druk?
We kunnen druk optellen door krachten op een oppervlakte op te tellen.
3.2. opblazen
- We blazen een luchtballon op.
- Waarom wordt de luchtballon groter?
- Waarom wordt de luchtballon gelijkmatig groter?

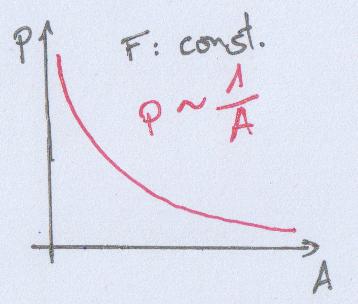
- proberen: harder opblazen
3.3. barsten
- Waarom horen we een geluid?
3.4. proef
- Hoe kunnen we de luchtballon groter maken zonder te blazen?
4. druk in een ideaal gas
- aantal deeltjes
- volume
- temperatuur (deeltjesbeweging)
5. Toepassing: Spekjes!
6. Samenvatting
- atmosfeer: druk \(\approx 101\ kPa = 1\ atm\)
- beginsel/principe van Pascal
- druk is een scalair
- luchtballon: samenhang druk/oppervlakte, krachtenevenwicht
- gasdeeltjes
vorige les \(\quad\) volgende les