Herhaling: Stroom en Spanning
1. Organisatie :
- voldende week: oefening zelfstandig; vragen via “forum”
- Toets: 4/3/2024
2. TL;DR
(wat moeten jullie vandaag onthouden?)
- Voltmeter schakel je parallel, Appèremeter in rij
- Spanning: is “Energie per lading”, een “conservatieve” energie, analoog: gravitationele potentiele energie
- Wet van Ohm: \(U = R \cdot I\) (met alle symbolen en eenheiden)
3. Denken zoals een Wetenschapper!
4. Elektrostatisch Potentieel (Th3 H2.1 ↗72+)
4.1. conservatieve krachtvelden
- elektrostatisch potentieel = spanning = potentiele energie per lading
- analogie: potentiele gravitationele energie

In een statisch elektrisch veld is de potentiele elektrische energie (en daarom ook de spanning) op een bepaalde plek onafhankelijk van de weg of tijd.
Analogie met gravitatie: sta op een stoel, spring er af, ga weer op de stoel staan, spring opnieuw, … → zelfde potentiele gravitationele energie
4.2. stroomkring, gelijkstroom
per analogie:

De som van de elektrische potentiaalverschillen, rekening houdend met de stroomrichting, in elke gesloten kring in een netwerk is gelijk aan nul.
(zie hier)
Dit verklaart onder meer:
- (Th3 H4 ↗79)
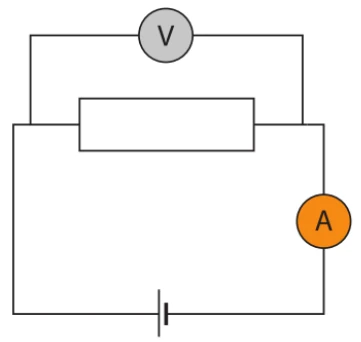
- (Th3 H4 ↗87)
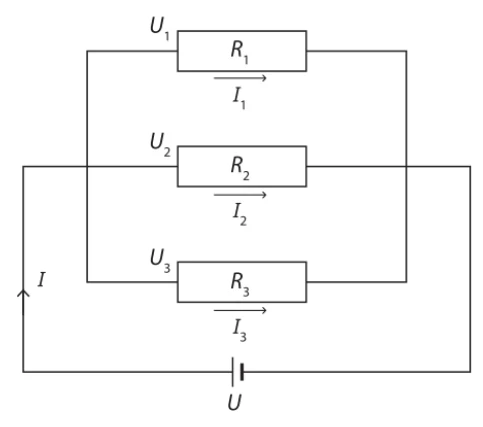
5. Wet Van Ohm (Th3 H2.1 ↗80)
- ezelsbrug: URIne
\[U = R \cdot I\]
starring:
- lading \(Q\) in Coulomb \(\left[C\right]\) (SI-eenheid)
- stroomsterkte \(I\) in Ampère \(\left[A = \frac{C}{s} \right]\)
- electrische spanning \(U\) in Volt \(\left[V = \frac{J}{C}\right]\)
- electrische weerstand \(R\) in Ohm \(\left[\Omega = \frac{V}{A}\right]\)
De minder bekende neef van Ohm:
- electrische geleidbaarheid \(G = \frac{1}{R}\) in Siemens