Arbeid en Energie
1. Arbeid: Voorbeelden (Th2 H1.2 LB↗45)
(voor jullie om te doordenken)
1.1. strandbal
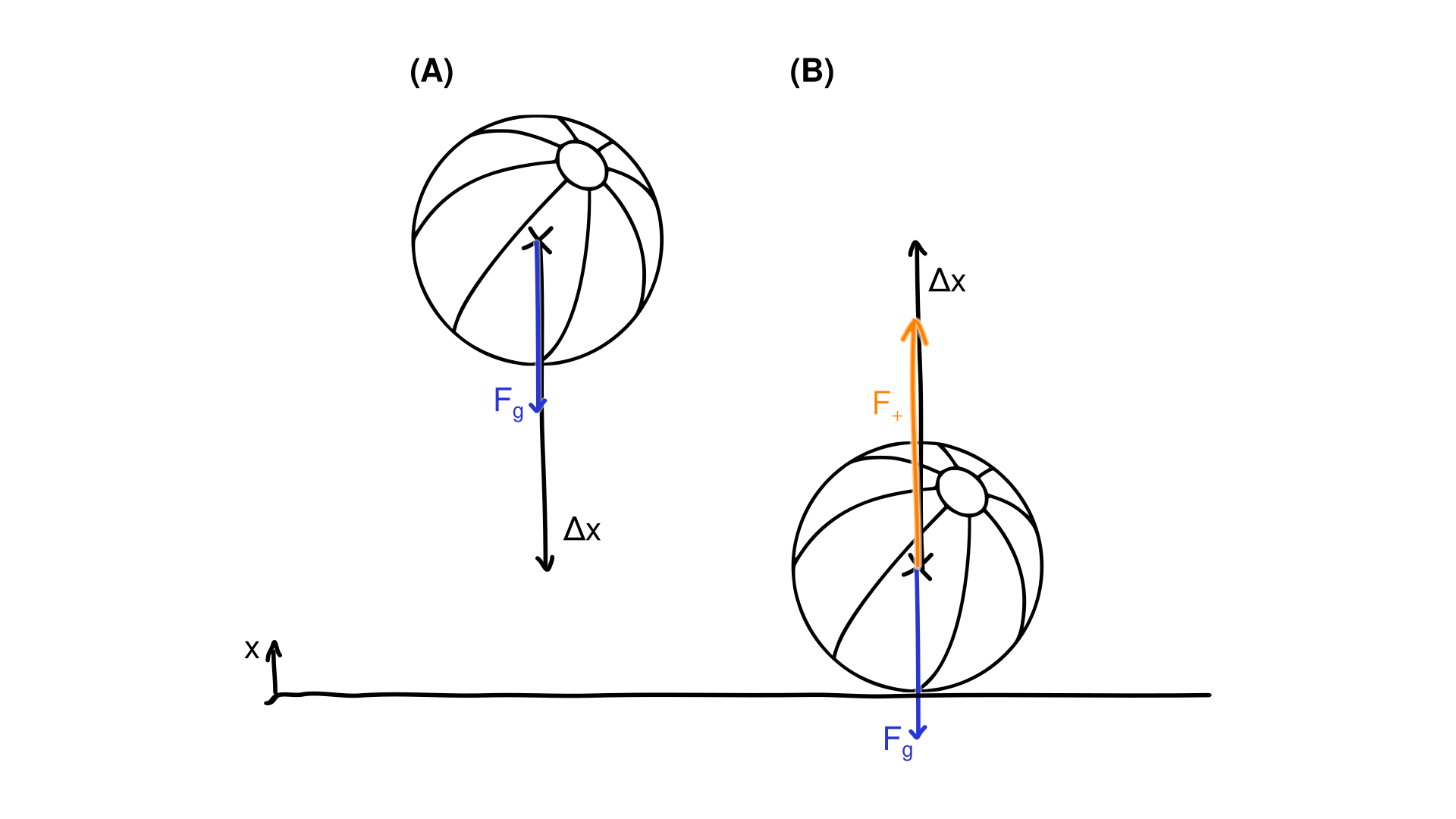 [2]
[2]
1.2. doos op tafel
massa: 1kg
- zit stil
- glijdt wrijvingsloos, \(a=0\frac{m}{s^2}\)
- verschuiven \(1m\) met versnelling \(a=10\frac{m}{s^2}\)
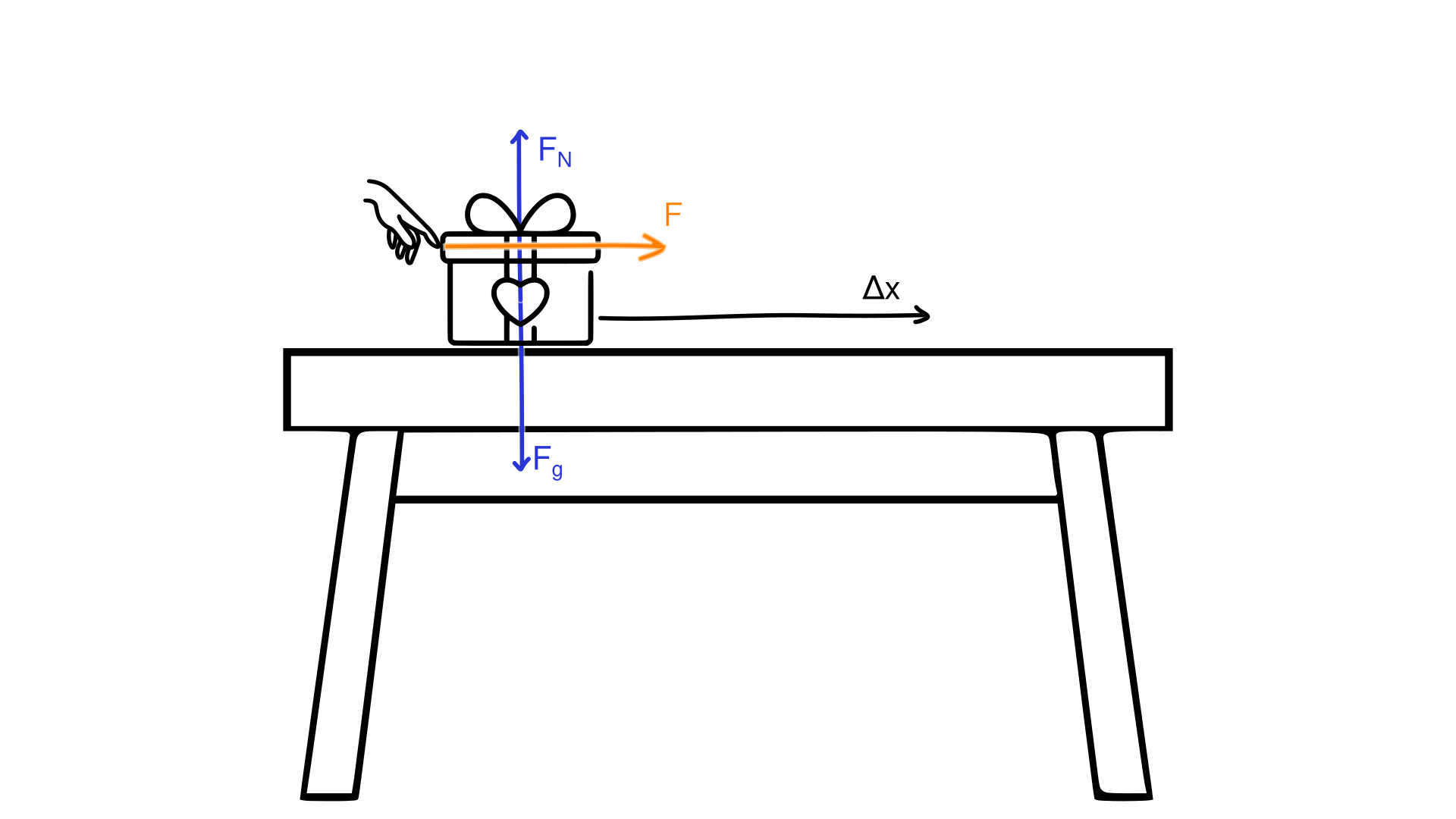 [2]
[2]
1.3. lift
- instappen: staat stil
- versnellen: gaat omhoog met \(a=5\frac{m}{s^2}\)
- gelijkvormig omhoogbewegen: \(a=0\frac{m}{s^2}\)
- vertragen: \(a=-5\frac{m}{s^2}\)
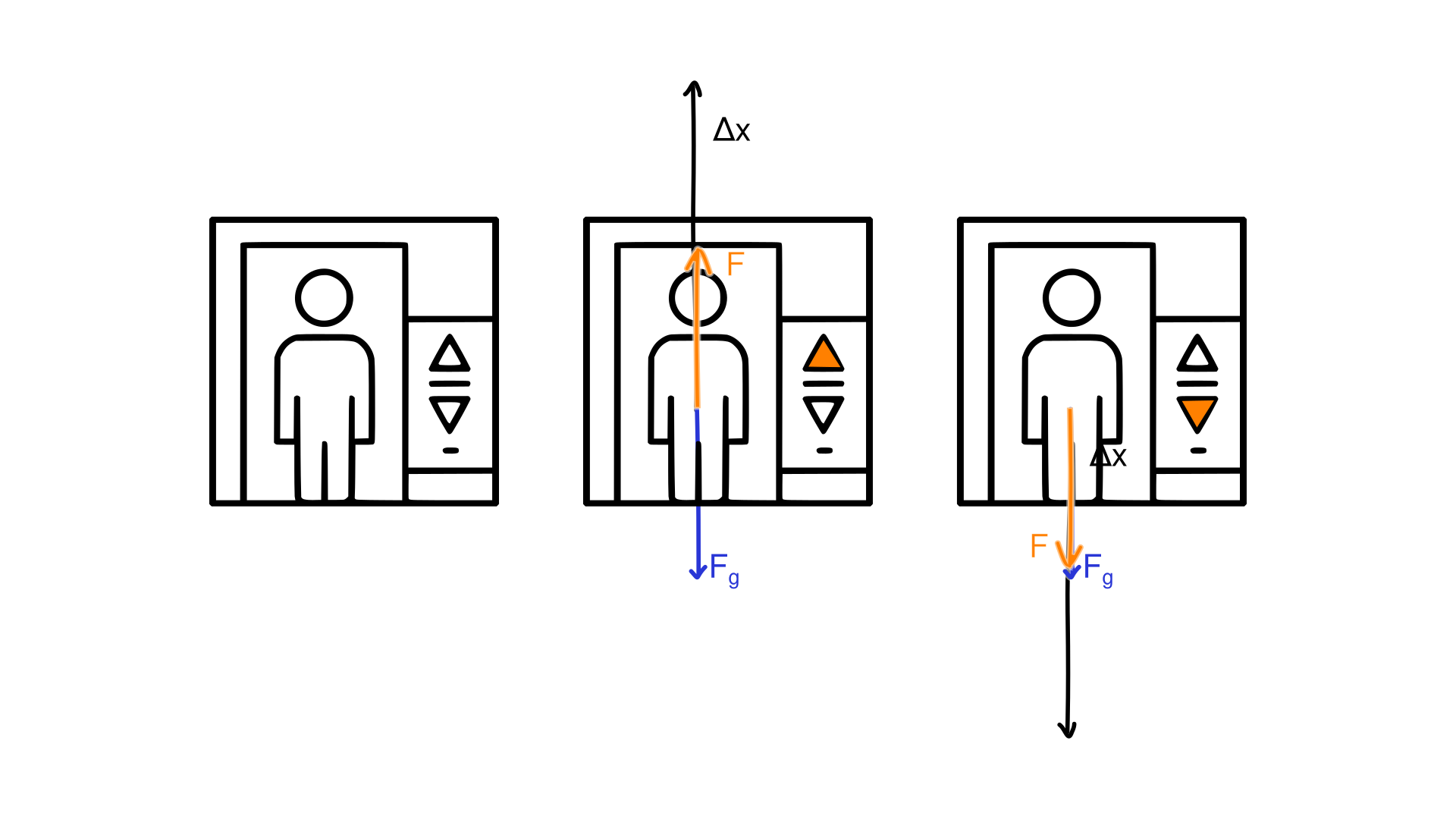 [2]
[2]
1.4. sneeuwsport
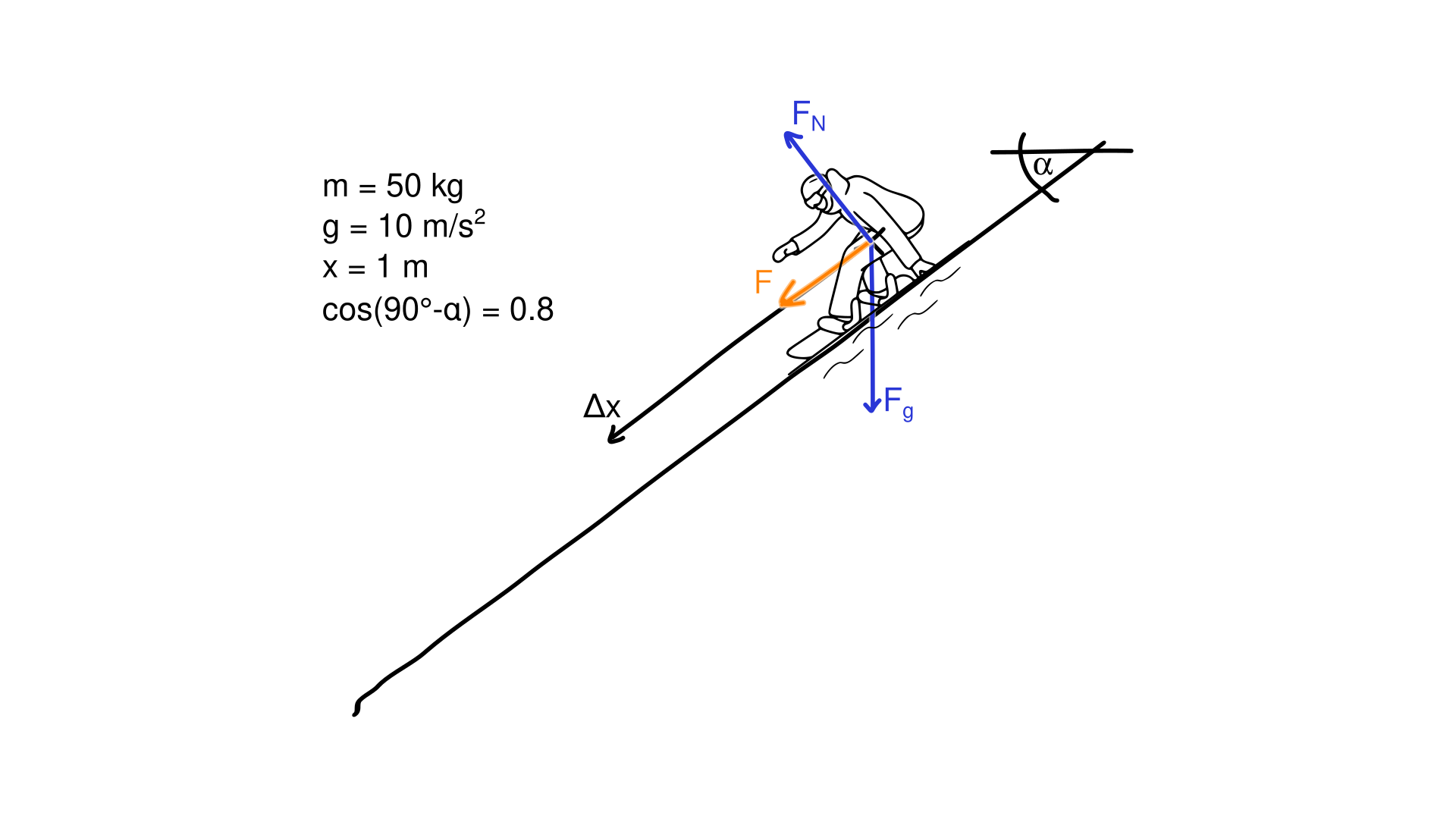 [2]
[2]
\[W = F\left| \Delta x \right| \cdot cos(\alpha ) \]
2. Mechanische Energie (Th2 H1.2 LB↗45)
2.1. Arbeid-Energie-Theorema
- arbeid is de omzetting van energie, arbeid is energie!
Bewijs: [bron: lecture by Walter Lewin]
- \[a=\frac{dv}{dt} \]
- \[F=ma=m\frac{dv}{dt}\]
- \[v=\frac{dx}{dt} \Leftrightarrow dx=v\cdot dt\]
- \[W_{AB}=\int\limits_{A}^{B} m\cdot a\cdot dx \]
- \[W_{AB}=\int\limits_{A}^{B} m \frac{dv}{dt}\cdot v dt = \int\limits_{v_A}^{v_B} m\cdot v\cdot dv \]
- \[W_{AB} = \left\ \frac{1}{2}mv^2 \right|_{v_A}^{v_B} = \frac{1}{2}mv_B^2 - \frac{1}{2}mv_A^2 = \frac{m}{2}\left(v_B^2-v_A^2\right)\]
En, zie beneden:
\[E_k = KE = \frac{1}{2}mv^2\] Kinetische Energie = Bewegingsenergie
bijzondere eenheid\(^*\): Joule
\(1J = 1Nm\)
(\(^*\) … maar eigenlijk is het hetzelfde als Nm. )
2.2. Potentiele Gravitationele Energie
\(E_p = m\cdot g\cdot h\)
- Zoals arbeid!
- voorbeeld: LB↗45
2.3. Kinetische Energie
\(E_k = \frac{1}{2}\cdot m\cdot v^{2}\)
Voorbeeld: Pendulum!
2.4. Potentiele Elastische Energie
\(E_e = \frac{1}{2}\cdot k\cdot l^{2}\)
- met \(k\): veerkonstante, eenheid \(\frac{N}{m}\)
- ook een potentiele energie ⃪ potentiaal: “het gaat eer terug komen”
- beter: de energie is bepaald door die positie; maakt niet uit hoe het daar naartoe kwam
- (anders: bewegingsenergie)
3. Behoud van Energie (Th2 H1.1 LB↗39)
Formuleringen:
Energie kan niet worden gecreëerd of vernietigd, maar alleen omgezet van de ene in de andere vorm.
De totale hoeveelheid energie in een geïsoleerd systeem blijft te allen tijde constant.
De totale energie van het universum is constant.
(en trouwens: materie is ook maar energie → behoud van massa)
Drie soorten van systemen:
- open systeem (mok)
- gesloten systeem (mok met deksel)
- geïsoleerd systeem (thermos)
4. Demonstratie: Slinger

vorige les \(\quad\) volgende les