Druk: Crash Course Formules
1. Level 0: De Vergelijking
1.1. “gelijk aan”
\[x = y\]
- Het symbol `=` betekent: alles wat links staat is hetzelfde als alles wat rechts staat!
- Hier: \(x\) is hetzelfde als \(y\); overal waar \(x\) staat mogen we \(y\) denken.
1.2. omkeeroperaties
- \(+ \leftrightarrow -\)
- \(\cdot \leftrightarrow :, \frac{\square}{\square}\)
- \(e^\square \leftrightarrow ln(\square ) \)
- afgeleide \(\leftrightarrow\) integraal
…
2. Level 1: Druk bij Vaste Stoffen
2.1. onthouden: één form van de formule!
Wij kunnen een formule omvormen.
- Voorbeeld: druk \(p\) (engels: “pressure”) is de quotient van kracht \(F\) en oppervlak \(A\)
\[p = \frac{F}{A}\]
- vermenigvuldigen met \(A\)
\[p\cdot A = F\]
Tipp: onthouden door een woord of zin te maken, hier bv. “fap”!
- delen door \(p\)
\[A = \frac{F}{p}\]
Leerdoel: Je moet elke formule naar alle kanten kunnen omvormen!
2.2. onthouden: eenheid!
De eenheid van de druk is
\[\left[p\right] = \frac{N}{m^2} =: Pa\] (“Pascal”)
Toepassing: zie beneden!
2.3. voorbeeld
- scheepsraampje
We meten op een patrijspoort (scheepsraampje, meestal rond) onder water een druk van \(10^5\ Pa\). Het glas heeft een oppervlakte \(1\ m^2\). Hoe groot was de kracht van het water?
 [▶]
[▶]
- zand (LP Th1 H1 ↗12)
Een persoon heeft een gewicht van \(800\ N\) en een totale voetoppervlakte van \(0,4\ m^2\). Hoe groot is de druk die zij uitoefent op het zand als zij met beide voeten naast elkaar staat?
 [Photo by Irina Popovich on Unsplash ]
[Photo by Irina Popovich on Unsplash ]
3. Level 2: Druk bij Vloeistoffen
3.1. vergelijkingen combineren
- stap: verzamel alle formules
gewichtskracht: \( F=m\cdot a\) specifieke massa = dichtheid: \( \rho = \frac{m}{V}\) druk: \( p=\frac{F}{A} \) volume: \( V=A\cdot h \) - stap: check de eenheiden!
schrijf boven met een kleur de eenheiden bij!
- stap: invoegen
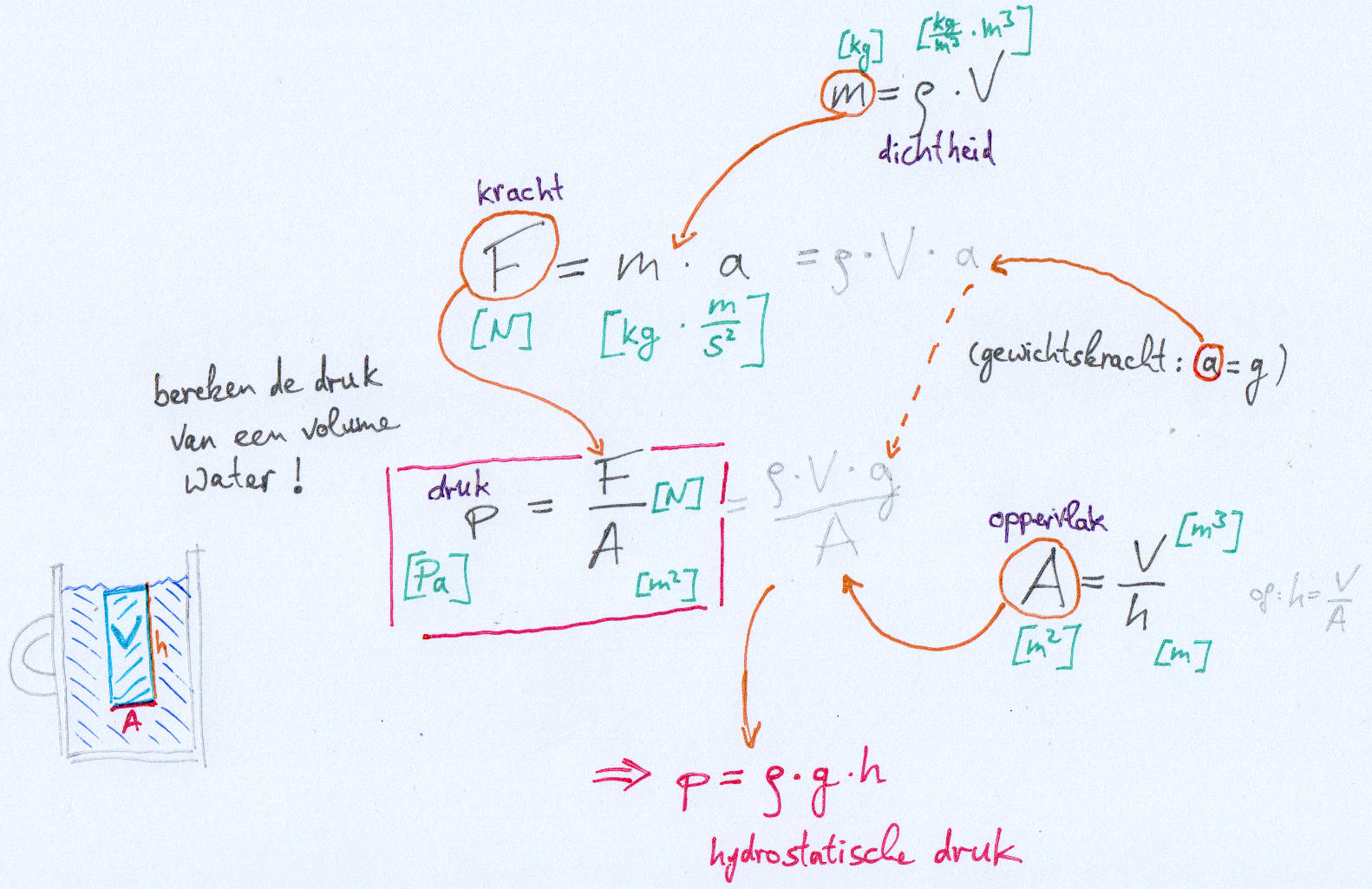
hydrostatische druk:
\[p_{hs} = \rho \cdot g \cdot h\]
3.2. oefening: “scuba-diving”
(= duiken met een ademautomaat)
 [▶]
[▶]
Een duiker duikt op \(h=10\ m\) diepte onder water. Hij meet een hydrostatische druk van \(p=100\ kPa\). De valversnelling is bekend met \(g = 10 \frac{m}{s^2}\).
- Bereken de dichtheid van water!
4. Level 3: Druk bij Gassen
4.1. ideaal gas
4.2. oefening 1: eenheiden
Welke eenheid heeft de gasconstante R?
4.3. oefening 2: formules begrijpen
Van welke faktoren hangt de gasdruk af, en hoe (evenredig)?
5. Samenvatting
- onthouden: één formule, eenheiden, symbolen
- vaardigheden: formules omvormen, invoegen, eenheiden verifiëren
- druk: drie formules (toepassing volgd)
vorige les \(\quad\) volgende les
 [
[